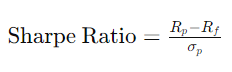Understanding the Sharpe Ratio: A Key Metric for Investment Performance

When it comes to evaluating the performance of an investment, the Sharpe Ratio stands out as one of the most popular and widely used metrics. Developed by Nobel laureate William F. Sharpe, this ratio helps investors understand the return of an investment compared to its risk. Let's dive into what the Sharpe Ratio is, how it's calculated, and why it's important.
What is the Sharpe Ratio?
The Sharpe Ratio measures the performance of an investment compared to a risk-free asset, after adjusting for its risk. The higher the Sharpe Ratio, the better the risk-adjusted performance of the investment. Essentially, it helps investors determine whether an investment's returns are due to smart decisions or excessive risk.
The Sharpe Ratio Formula
The formula for calculating the Sharpe Ratio is:
Where:
- Rp = Expected return of the investment
- Rf = Risk-free rate of return
- σp\sigma_p = Standard deviation of the investment's returns (a measure of risk)
Sample Calculation
Let's consider an example to understand how the Sharpe Ratio is calculated.
Assume the following:
- The expected annual return of an investment (Rp) is 10%.
- The risk-free rate (Rf) is 2%.
- The standard deviation of the investment's returns (σp\sigma_p) is 15%.
Plugging these values into the formula:
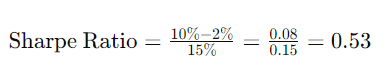
In this example, the Sharpe Ratio is 0.53. This means that for every unit of risk taken, the investment is expected to yield 0.53 units of excess return over the risk-free rate.
Why is the Sharpe Ratio Important?
The Sharpe Ratio is a crucial metric because it allows investors to:
- Compare the risk-adjusted returns of different investments.
- Determine whether an investment's returns are due to skill or excessive risk-taking.
- Make informed decisions by considering both the returns and the risk associated with an investment.
Limitations of the Sharpe Ratio
While the Sharpe Ratio is a valuable tool, it has its limitations:
- It assumes returns are normally distributed, which might not always be the case.
- It doesn't distinguish between upside and downside volatility.
- It relies on historical data, which might not predict future performance accurately.
Conclusion
The Sharpe Ratio is an essential metric for investors looking to evaluate the risk-adjusted performance of their investments. By considering both returns and risk, it provides a more comprehensive view of an investment's performance. However, like any metric, it should be used in conjunction with other tools and analysis for a well-rounded investment decision.